漫画算法-树
树和二叉树
树
许多逻辑关系并不是简单的线性关系,常常存在一对多,多对多的情况。树和图就是典型的非线性数据结构。
比如“家谱”是一个树,企业的职级关系是一个树。一本书的目录也是一个树。
定义:树是 n (n >= 0)个节点的有限集。当 n = 0 时,称为空树。在任意一个非空树中,有如下特点:
- 有且只有一个特定的称为根的节点。
- 当 n > 1 时,其余节点可分为 m(m > 0)个互不相交的有限集。每一个集合本身又是一个树,并称为根的子树。
几个概念:
父节点:某个节点的上一个节点。
孩子节点:某个节点衍生出来的节点。
兄弟节点:同一个父节点衍生出来的同级节点。
叶子节点:处于树的末端,没有子节点。
二叉树(binary tree)
这种树的每个节点最多有 2 个孩子节点。
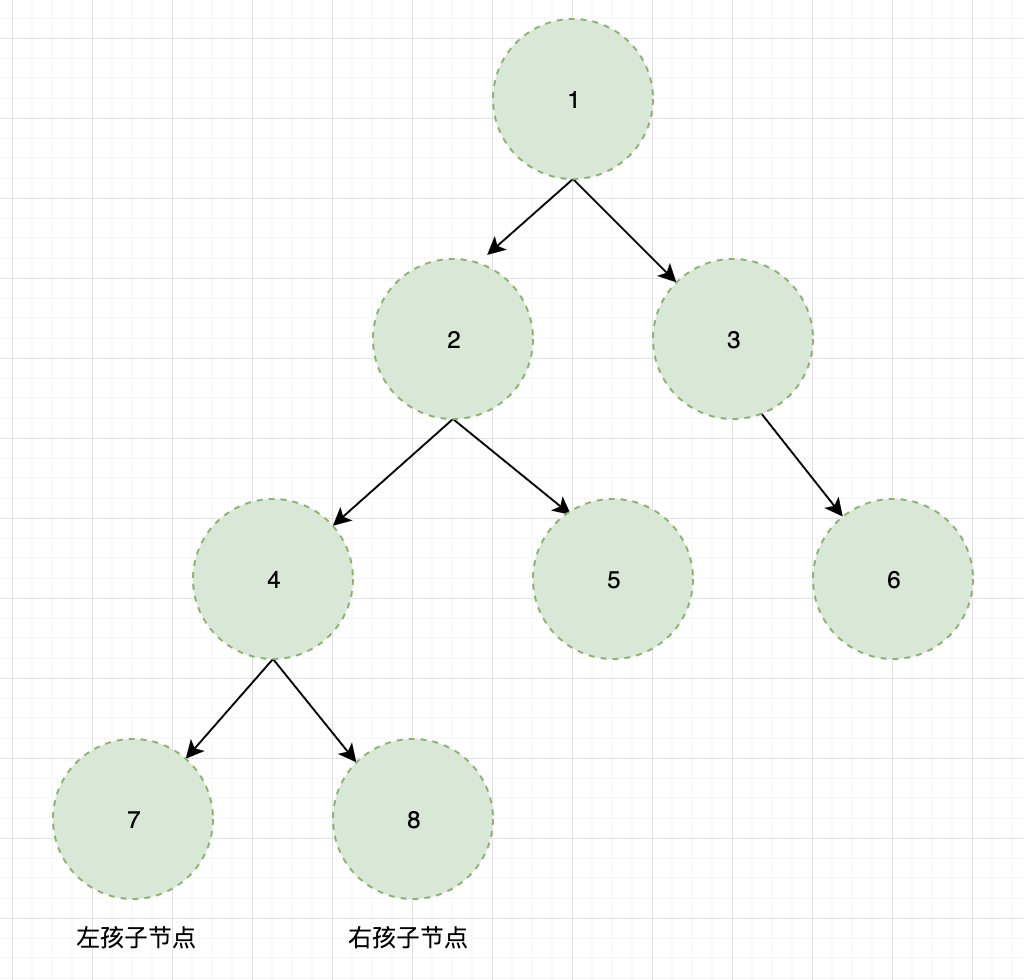
其中,左孩子节点和右孩子节点的顺序是固定的。
二叉树的两种特殊格式:
- 满二叉树:所有节点都是满的,且所有叶子节点都在同一层级上。要求所有节点都是满的。
- 完全二叉树:有 n 个节点,与相同深度的满二叉树的 1 到 n 个节点位置相同。只需保证最后一个节点之前的节点齐全。
二叉树属于逻辑结构,可以通过多种物理结构来表达:
- 链式存储结构
- 数组
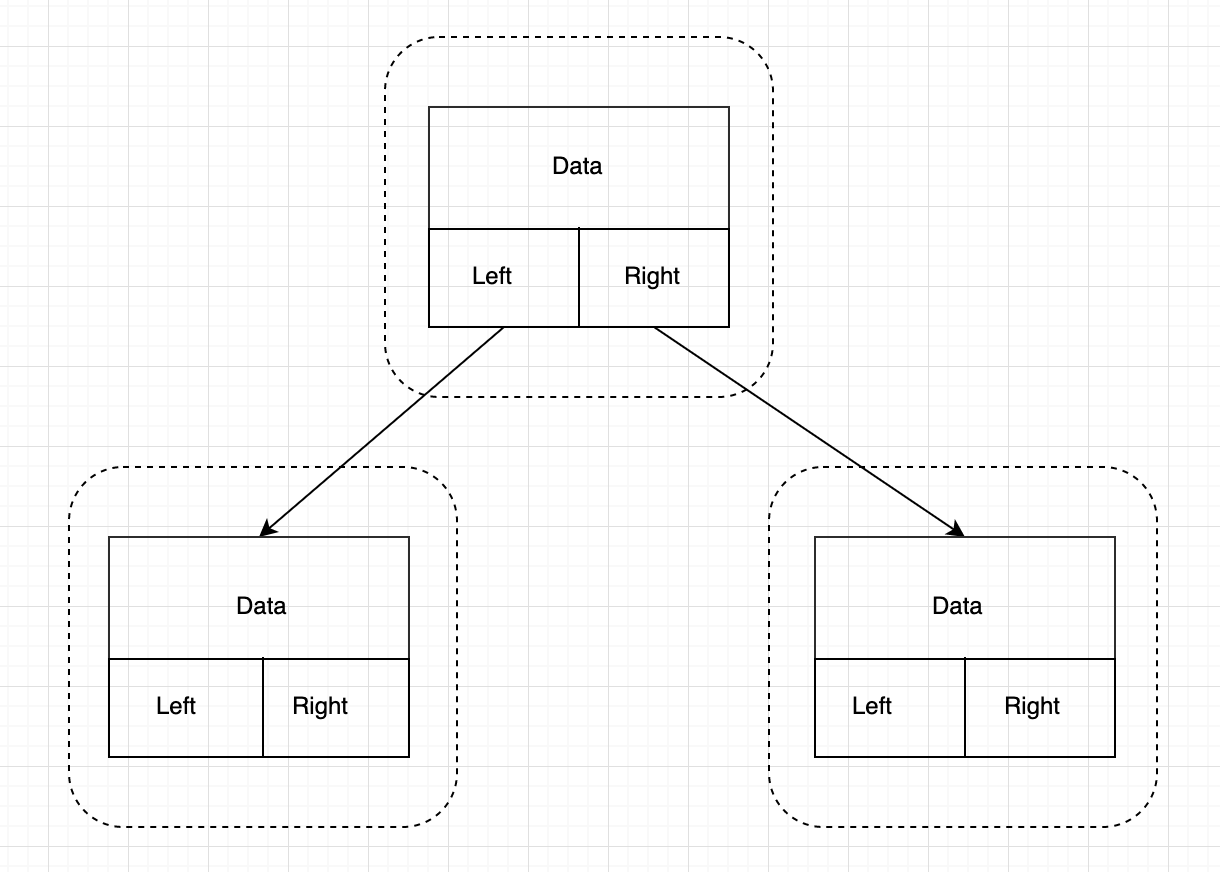
用链表表示:
包含了存储数据的 data 变量,指向左孩子的 left 指针,指向右孩子的 right 指针。
用数组表示:
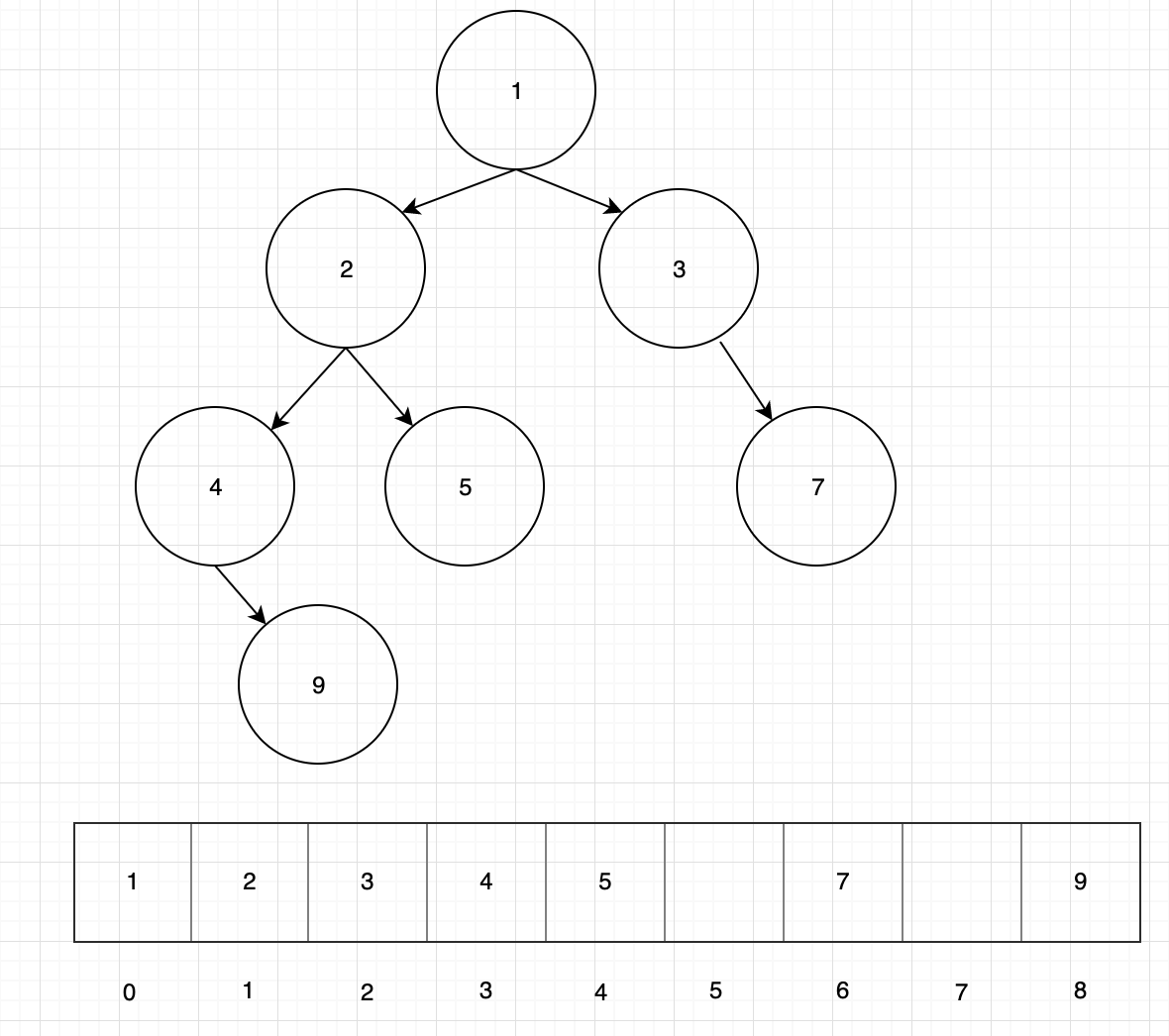
按照层级顺序把二叉树的节点放到数组相应的下标位置中。如果某个左孩子或右孩子缺失,数组相应的位置会空出来。
这样可以方便地定位孩子节点和父节点的位置。
leftChild = parent * 2 + 1;
rightChild = parent * 2 + 2;
parent = (leftChild - 1) / 2;
二叉树的应用
主要作用:查找操作和维持相对顺序。
1、查找
特殊的二叉树:二叉查找树(binary search tree)。
二叉查找树在二叉树的基础上加了几个条件:
- 如果左子树不为空,则左子树上所有节点的值都小于根节点的值。
- 如果右子树不为空,则右子树上所有节点的值都大于根节点的值。
- 左右子树都是二叉查找树
二叉查找树:
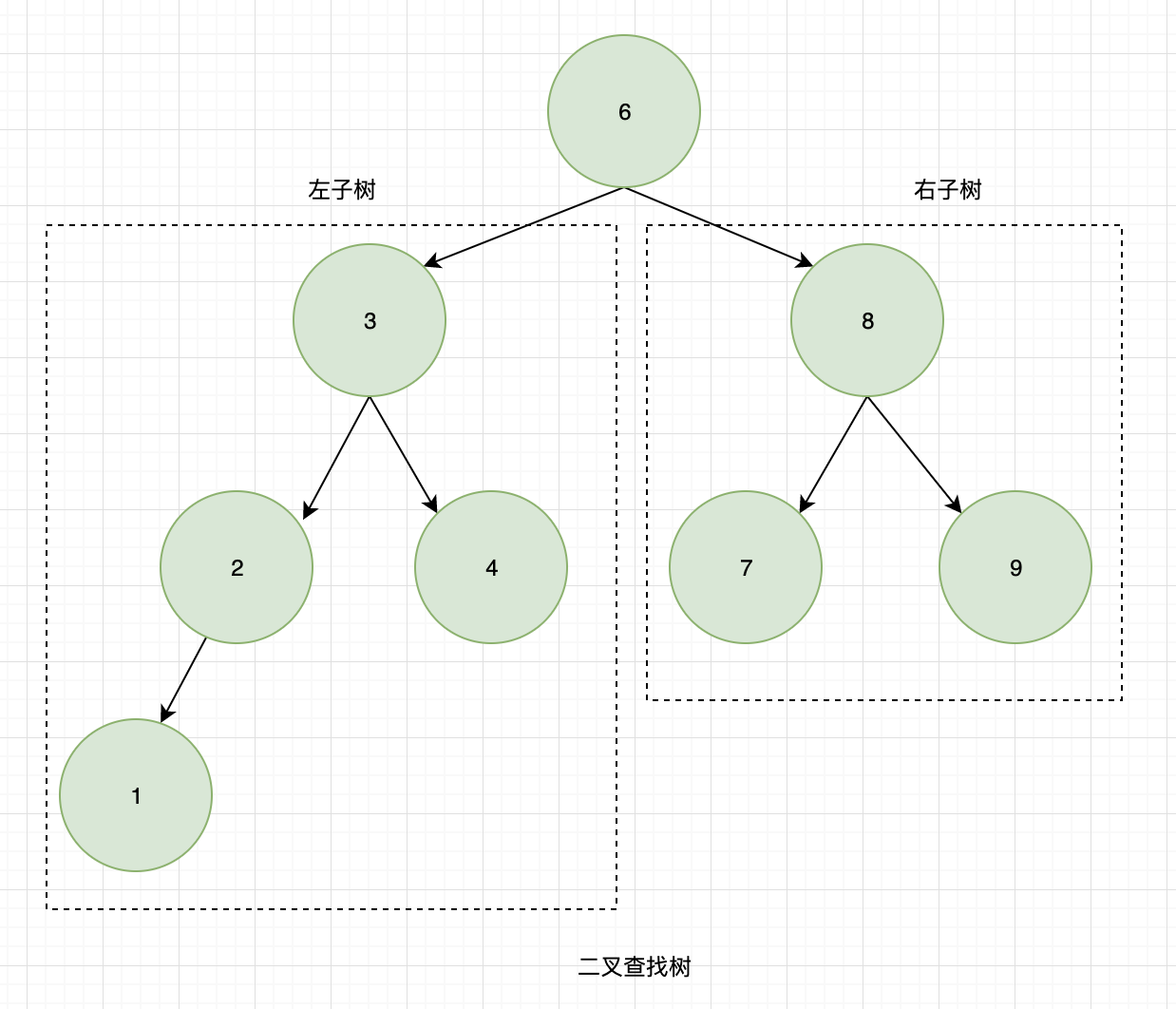
查找步骤:
- 比如查找 4,发现 4 < 6,查左子树,找到 3。
- 发现 4 > 3,查右子树,找到 4,查找完成。
对于一个节点分布相对均匀的二叉树来说,每次都是除以 2,所以算法复杂度是 O(logn)。
2、维持相对顺序
二叉查找树要求左子树的节点小于根节点,右子树的节点大于根节点,这样就保证了二叉树的有序性。
二叉树还有另一个名字:二叉排序树(binary sort tree)。
问题:在下面的二叉查找树中插入 9、8、7、6 等。
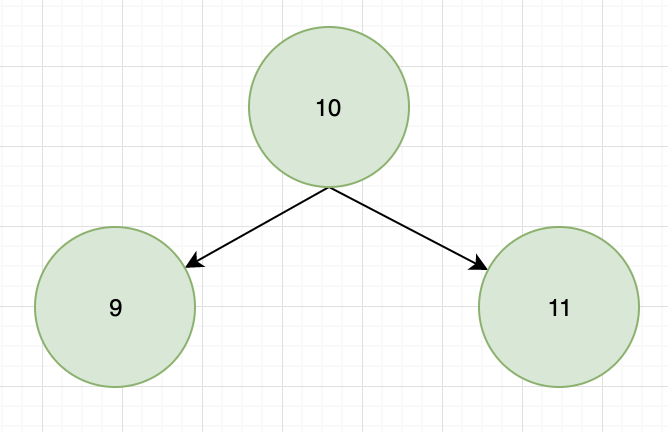
插入后:
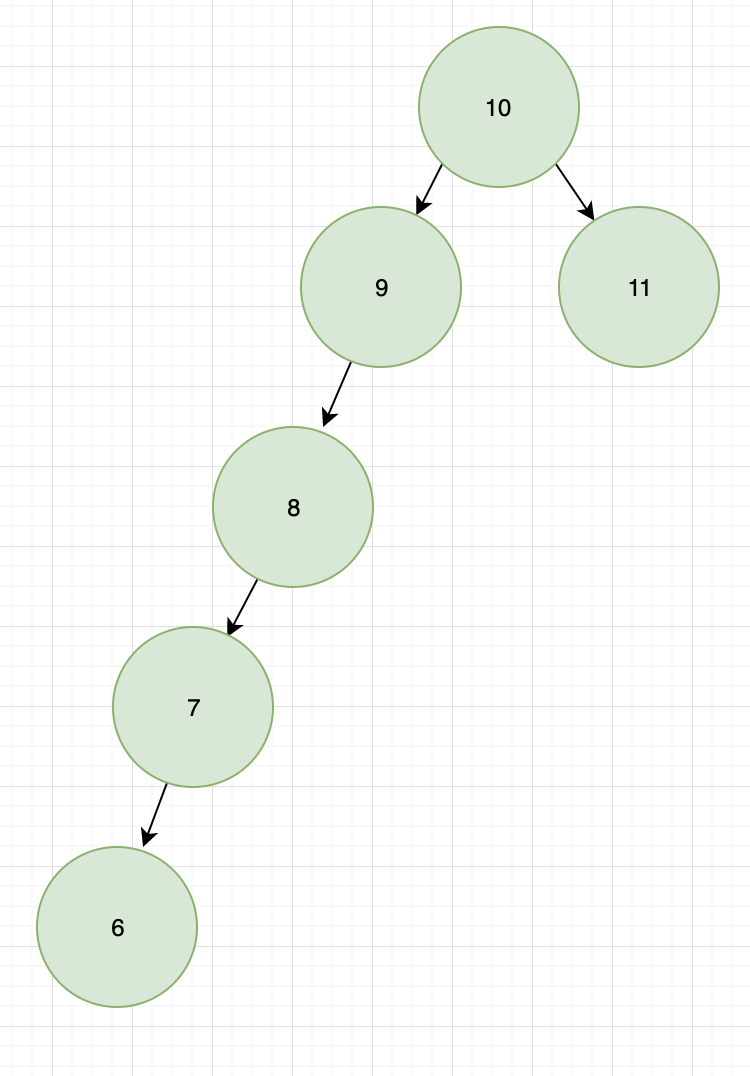
时间复杂度退化成了 O(n)。
解决这个问题,涉及到二叉树的自平衡:红黑树、AVL树、树堆等。
二叉树的遍历
为什么要研究遍历
在计算机中,遍历本身是一个线性操作,遍历具有同样结构的数组或链表,轻而易举。
但是二叉树是非线性数据结构,遍历时需要把非线性关联的节点转化成一个线性的序列,以不同的方式来遍历,遍历出的序列顺序也不同。
从节点之间位置关系的角度看,二叉树的遍历分为 4 种。
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
从更宏观的角度,二叉树的遍历归为:
- 深度优先遍历(前序遍历、中序遍历、后序遍历)
- 广度优先遍历(层序遍历)
深度优先遍历
深度优先:偏向于纵深的访问方式。
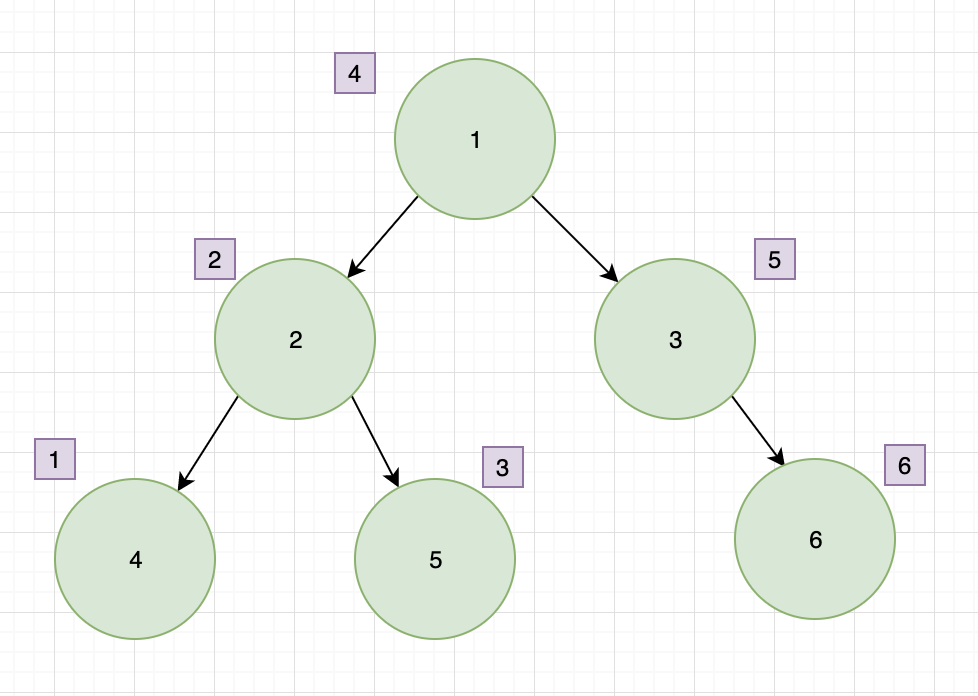
1、前序遍历
二叉树的前序遍历,输出顺序是根节点、左子树、右子树。
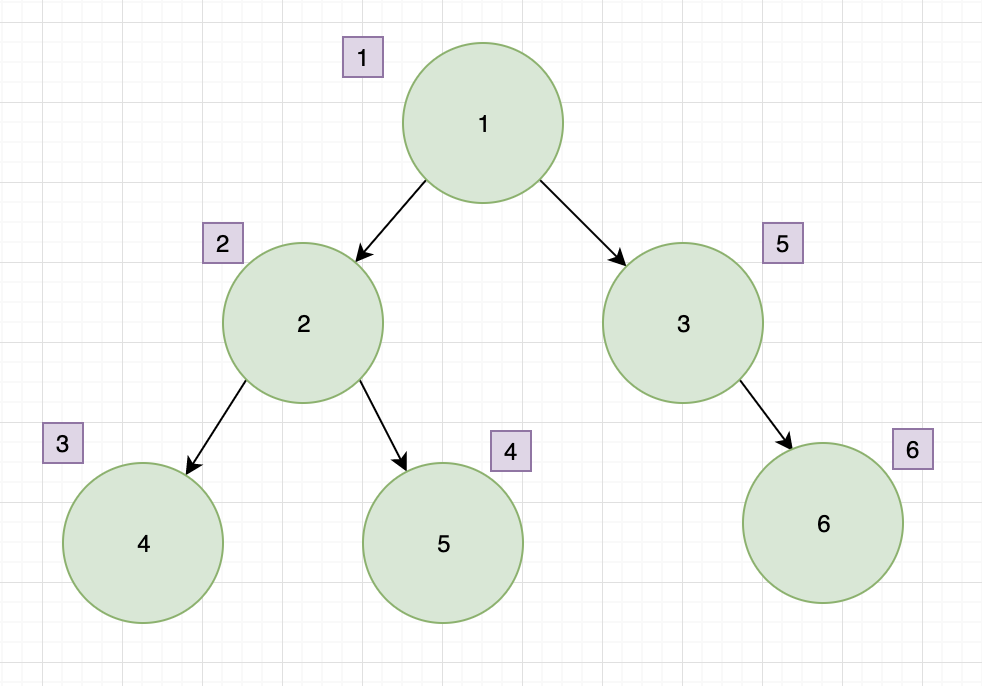
2、中序遍历
二叉树的中序遍历,输出顺序是:左子树、根节点、右子树。
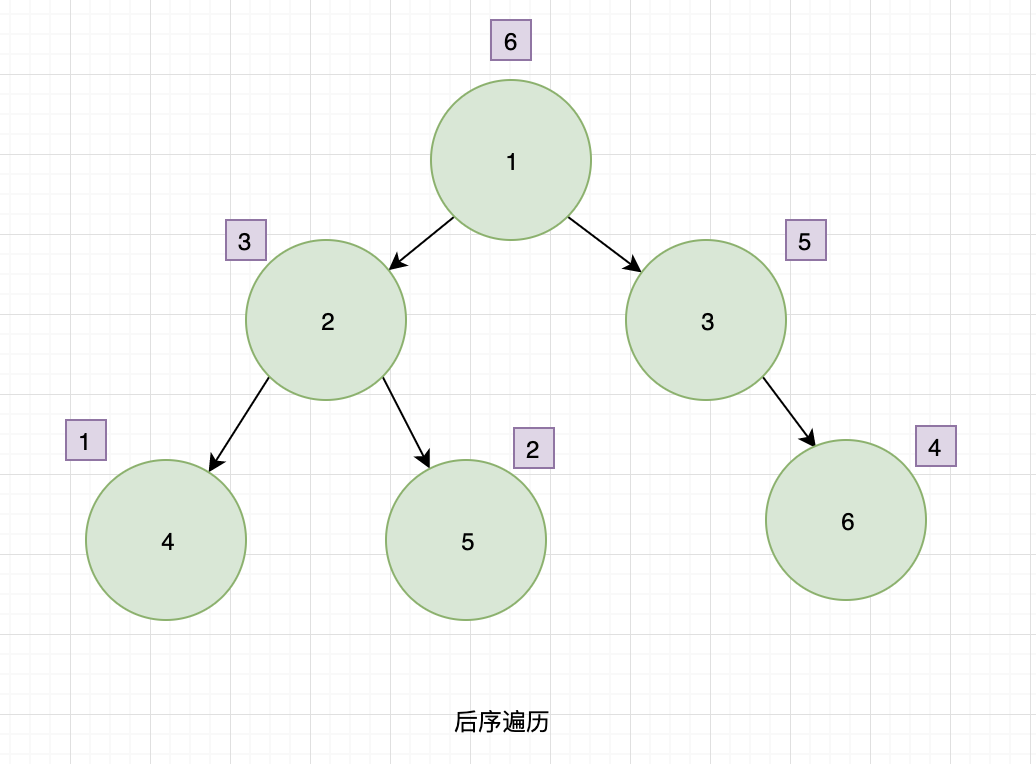
3、后序遍历
二叉树的后序遍历,输出顺序是:左子树、右子树、根节点。
构建二叉树 + 二叉树遍历:
递归方式
class TreeNode {
data;
leftChild;
rightChild;
constructor(data) {
this.data = data;
}
}
function createBinaryTree(list) {
let node = null;
if (list === null || !(list && list.length)) {
return null;
}
let data = list.shift();
if (data !== null) {
node = new TreeNode(data);
node.leftChild = createBinaryTree(list);
node.rightChild = createBinaryTree(list);
}
return node;
}
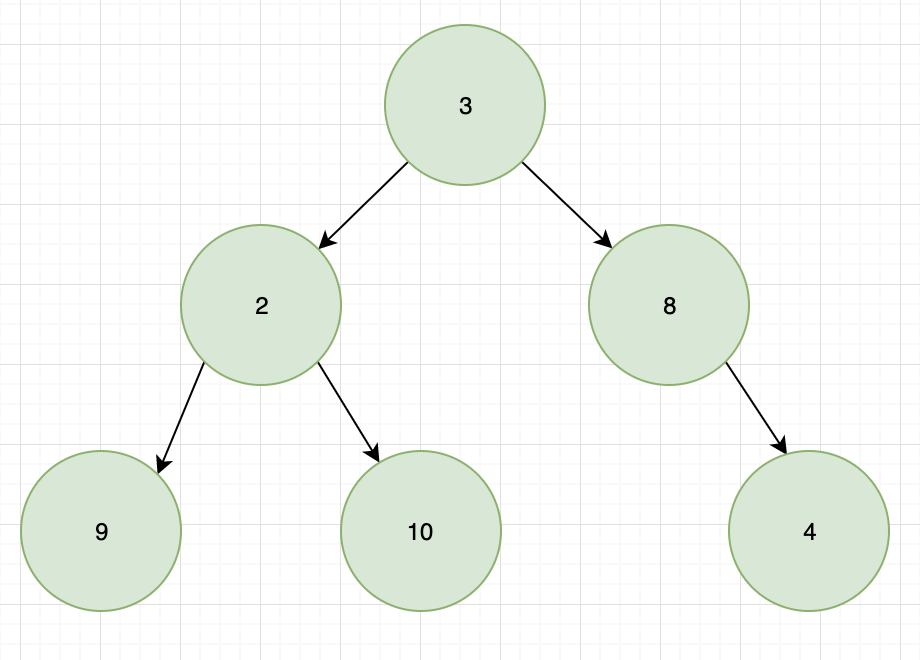
const list = [3, 2, 9, null, null, 10, null, null, 8, null, 4];
const treeNode = createBinaryTree(list);
构建二叉树结果:
// 前序遍历
function preorderTraversal(node) {
if (node === null) {
return;
}
console.log(node.data); // 输出根节点
preorderTraversal(node.leftChild); // 遍历左节点
preorderTraversal(node.rightChild); // 遍历右节点
}
// 中序遍历
function inorderTraversal(node) {
if (node === null) {
return;
}
preorderTraversal(node.leftChild); // 遍历左节点
console.log(node.data); // 输出根节点
preorderTraversal(node.rightChild); // 遍历右节点
}
// 后序遍历
function postorderTraversal(node) {
if (node === null) {
return;
}
preorderTraversal(node.leftChild); // 遍历左节点
preorderTraversal(node.rightChild); // 遍历右节点
console.log(node.data); // 输出根节点
}
console.log('前序遍历');
preorderTraversal(treeNode);
// 3
// 2
// 9
// 10
// 8
// 4
console.log('中序遍历');
inorderTraversal(treeNode);
// 2
// 9
// 10
// 3
// 8
// 4
console.log('后序遍历');
postorderTraversal(treeNode);
// 2
// 9
// 10
// 8
// 4
// 3
栈方式
// 前序遍历
function preorderTraversalWithStack(node) {
const arr = new Array();
let treeNode = node;
while (treeNode !== null || (arr && arr.length)) {
while (treeNode !== null) {
console.log(treeNode.data);
arr.push(treeNode); // 入栈
treeNode = treeNode.leftChild;
}
// 当前节点没有左孩子节点,将该节点弹出,访问该节点的右节点
if (arr && arr.length) {
treeNode = arr.pop(); // 弹出该节点,父节点设置为该弹出节点
treeNode = treeNode.rightChild; // 访问弹出节点的右孩子节点
}
}
}
preorderTraversalWithStack(treeNode);
// 中序遍历
function inorderTraversalWithStack(node) {
const arr = new Array();
let treeNode = node;
while (treeNode !== null || (arr && arr.length)) {
while (treeNode !== null) {
arr.push(treeNode);
treeNode = treeNode.leftChild;
}
if (arr && arr.length) {
treeNode = arr.pop();
console.log(treeNode.data);
treeNode = treeNode.rightChild;
}
}
}
inorderTraversalWithStack(treeNode);
// 后序遍历
function postorderTraversalWithStack(node) {
const arr1 = new Array();
const arr2 = new Array();
let treeNode = node;
while (treeNode !== null || (arr1 && arr1.length)) {
while (treeNode !== null) {
arr1.push(treeNode);
arr2.push(treeNode);
treeNode = treeNode.rightChild;
}
if (arr1 && arr1.length) {
treeNode = arr1.pop();
treeNode = treeNode.leftChild;
}
}
while (arr2 && arr2.length) {
treeNode = arr2.pop();
console.log(treeNode.data);
}
}
postorderTraversalWithStack(treeNode);
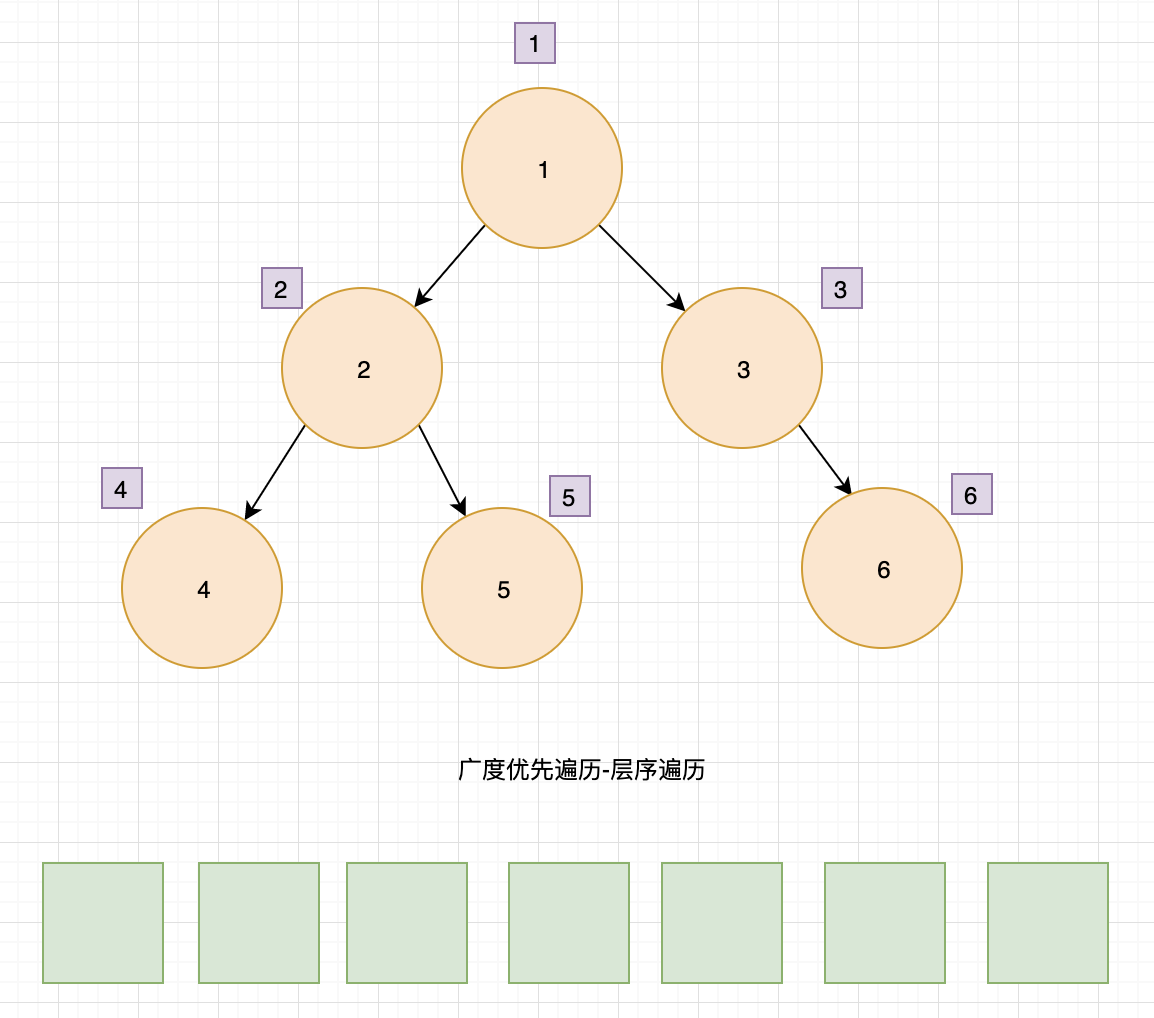
广度优先遍历
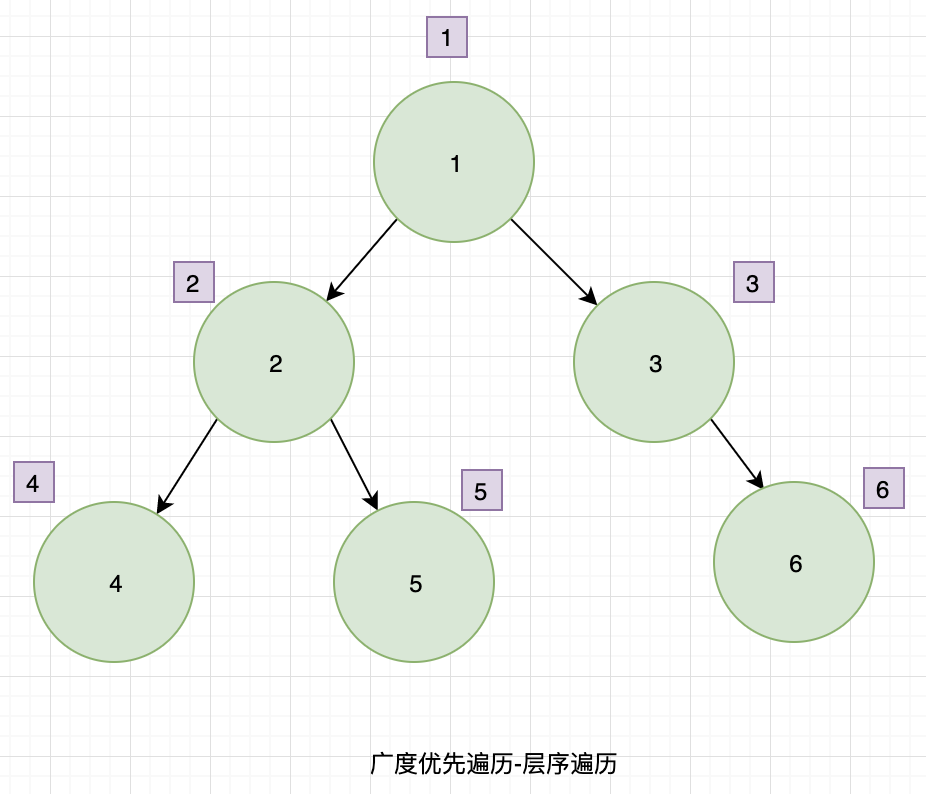
利用队列来实现遍历。
- 根节点 1 入队
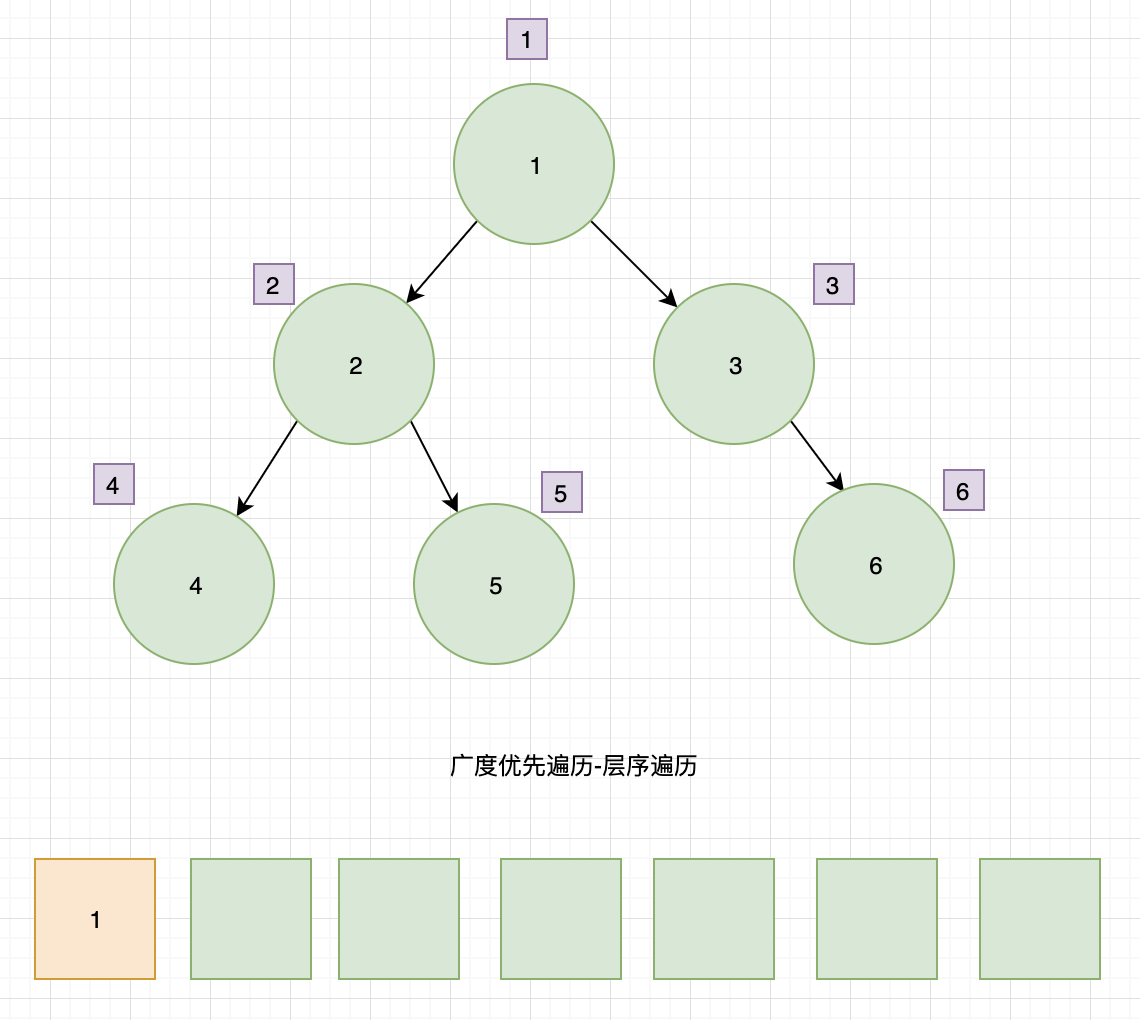
- 根节点 1 出队,输出节点 1,找到子节点 2、3,子节点 2、3 入队。
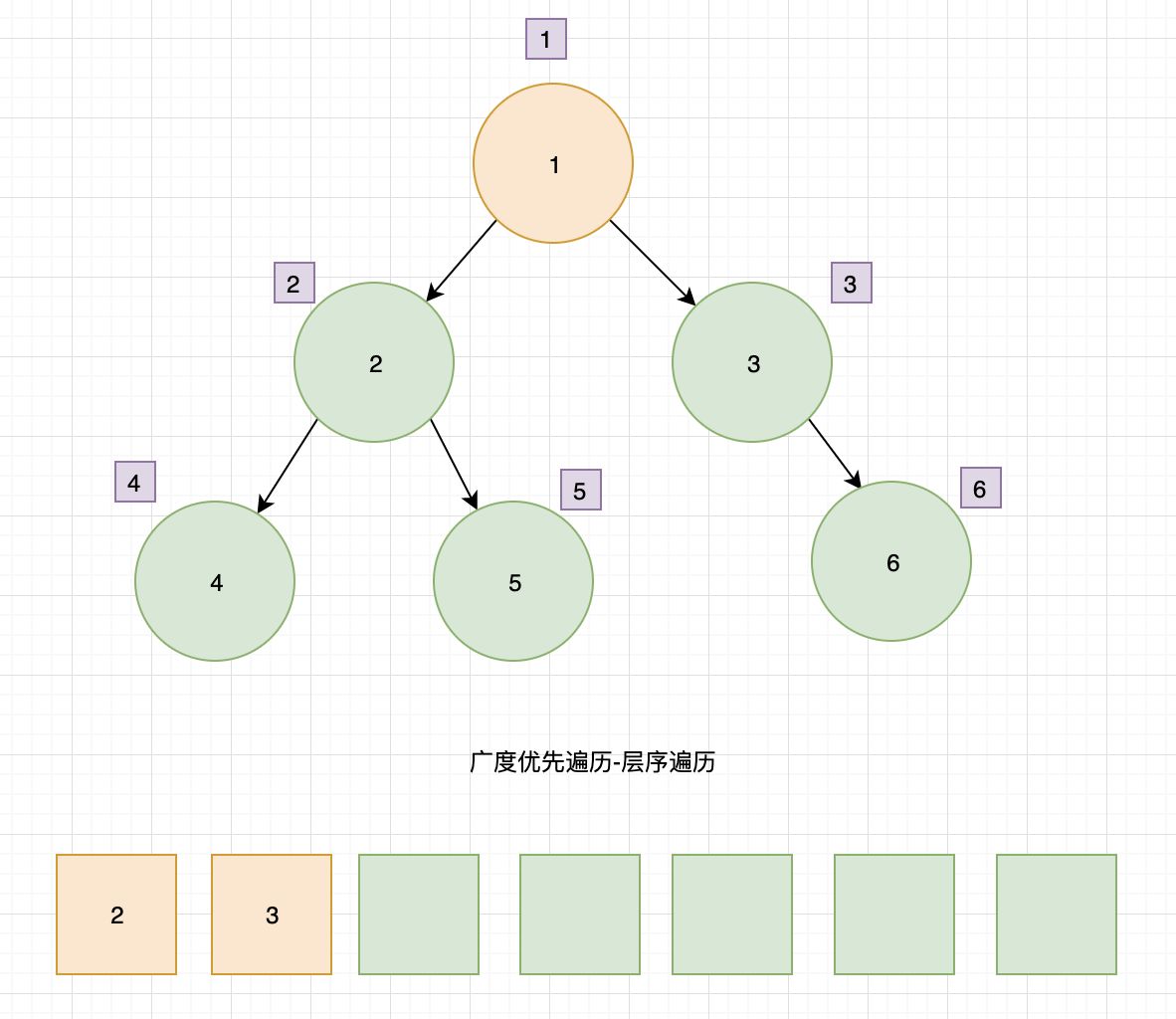
- 节点 2 出队,输出 2,找到子节点 4、5,4、5入队
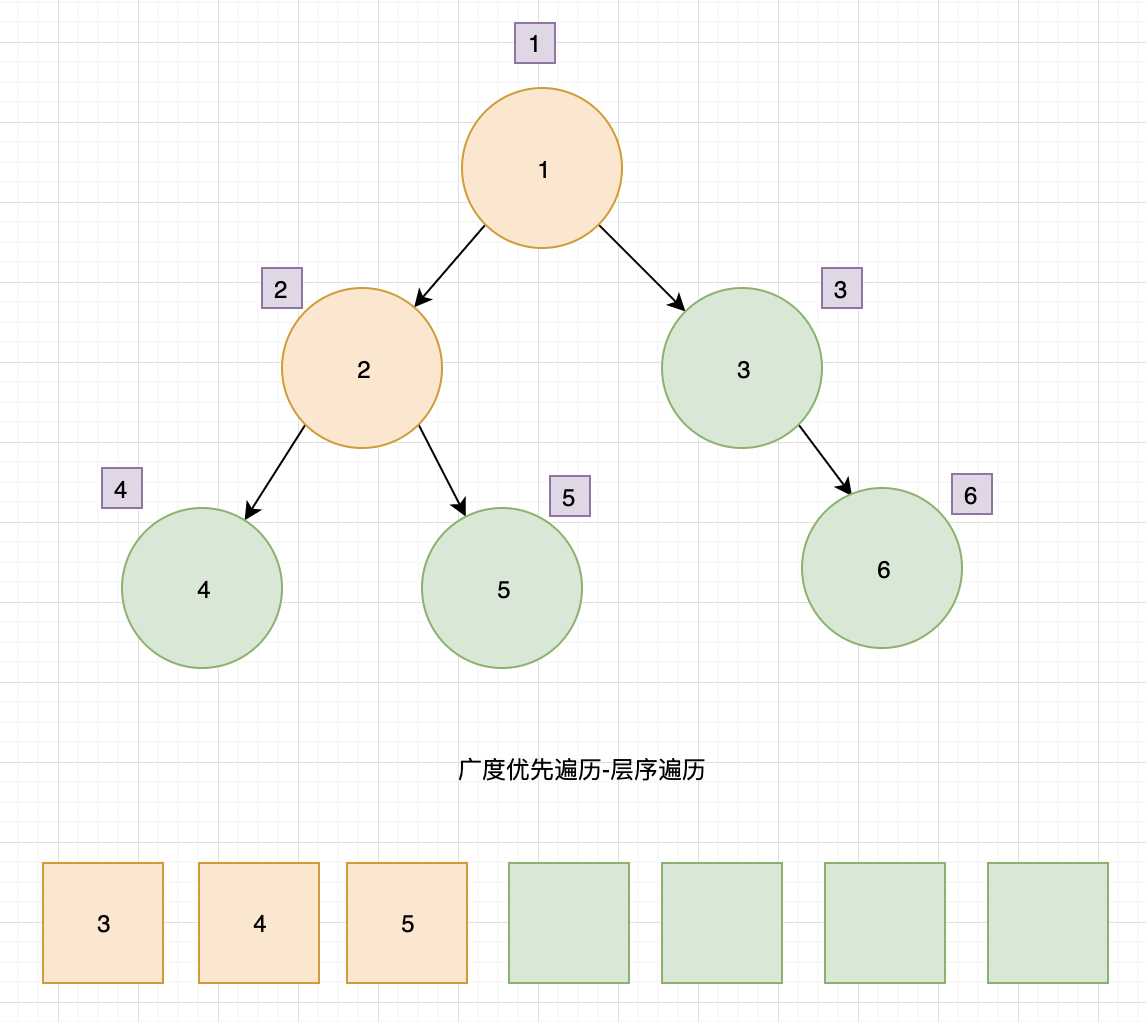
- 节点 3 出队,输出 3,找到子节点 6,节点 6 入队。
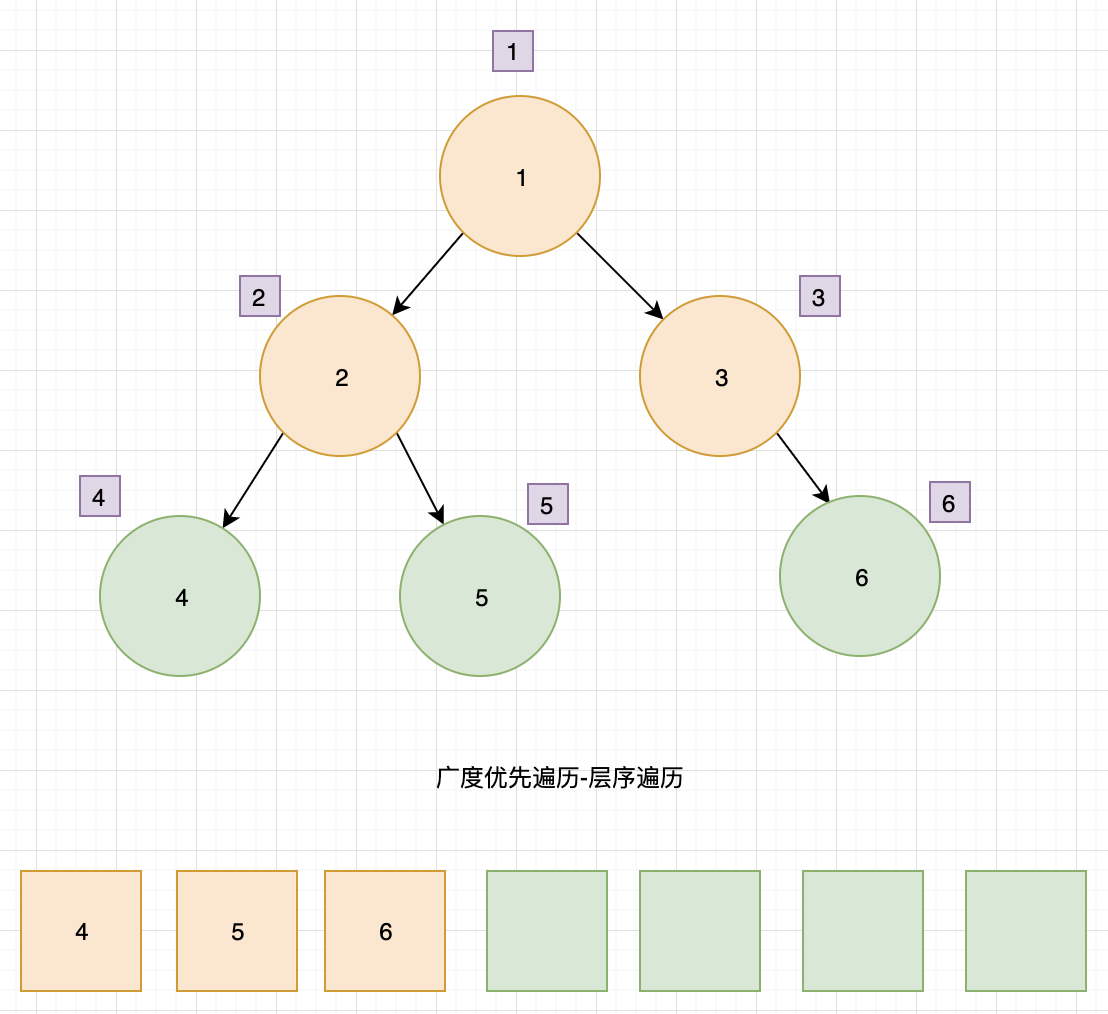
- 节点 4 出队,输出 4,没有子节点入队
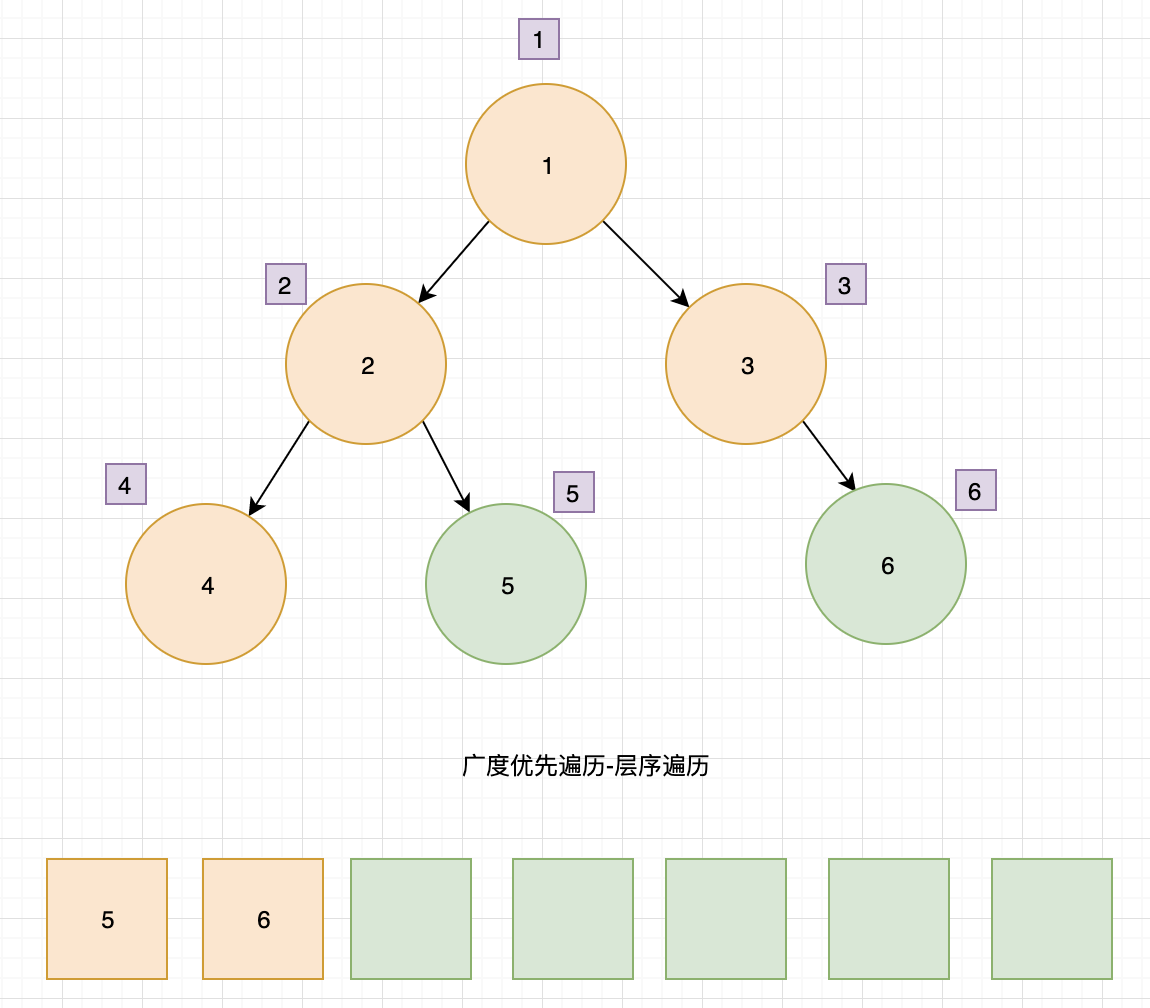
- 节点 5 出队,输出 5,没有子节点入队
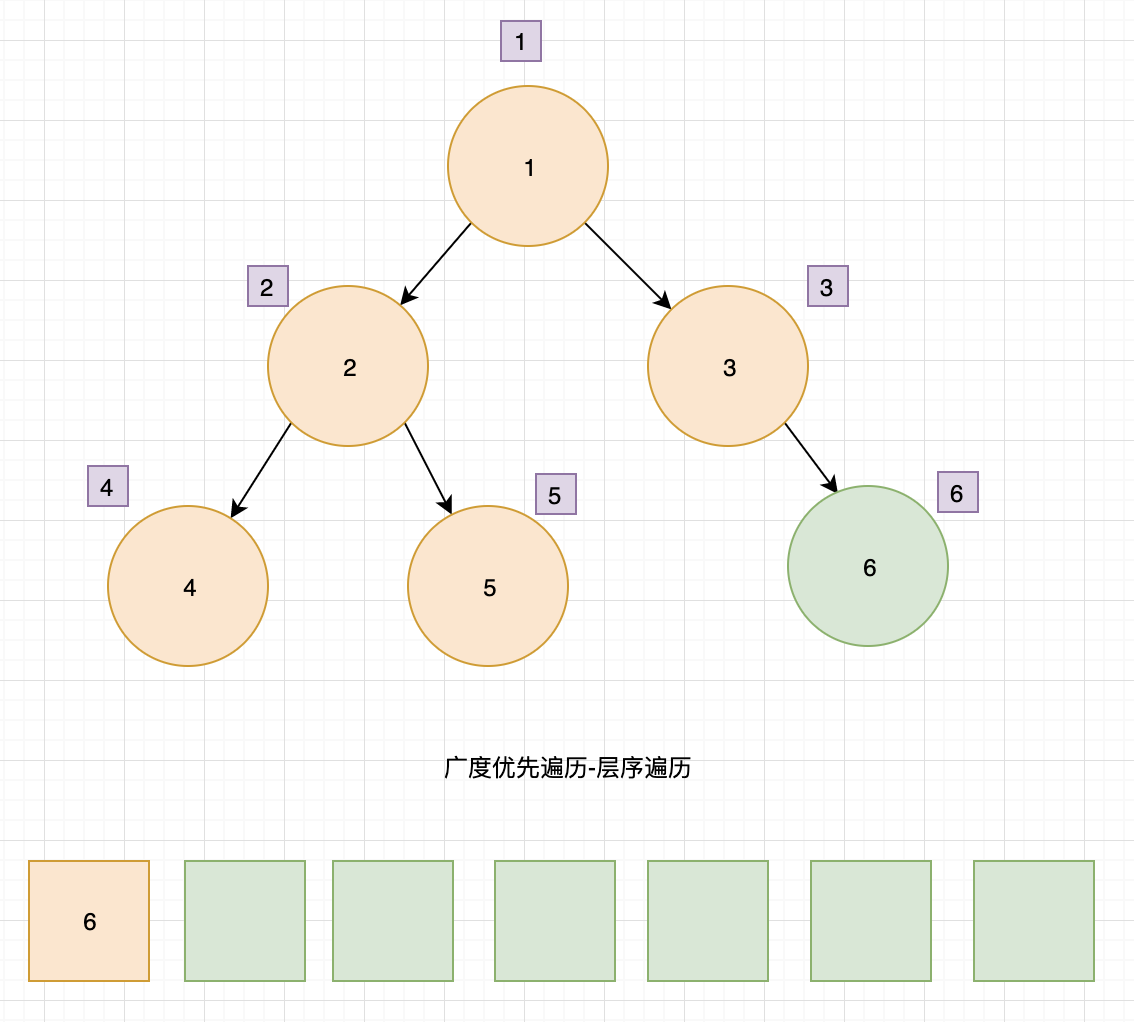
- 节点 6 出队,输出 6,没有子节点入队